Pólya's Random Walk Constants
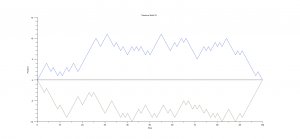
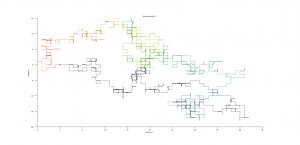
Imagine that a you are placed in the middle of an infinitely large field, blind folded. With nothing better to do, you spin around to face a random direction and begin walking. At random intervals of time you are compelled to stop and face another random direction, and continue to follow this process forever, never seeing where you're walking.
What is the likelihood that they'll end up at the exact location you started? Intuitively, the chance of this should almost surely be zero. With an infinite number of other places to go, arriving back at the origin should become less and less likely as time goes on.
The answer, it turns out, is that you're 100% guaranteed to end up where you started.
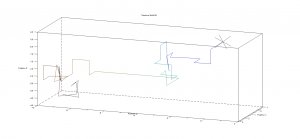
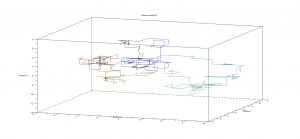
This surprising result was proved by Pólya in 1921, and holds true for 1 and 2 dimensions. However, at 3 dimensions and above, the chances of returning to the starting location drop dramatically.
This process is called a random walk. Below are images of such random walks, generated programmatically in SciLab. The SciLab file is available for download, and contains several configurable options.